Norms – A Small Primer on the Use of Norms for Assessment
Norms provide a useful way of selecting the best of what is available in a particular situation (economic crisis) or environment (lack of talent in a locality), but does this in line with the recruitment targets of the organisation. In actual terms, norms are a way of benchmarking the applicants against others of a comparable position, to help obtain some sense of their potential.
Imagine a small population of experts who are all in demand for a particular role where the recruitment process expects a certain level of technical proficiency for the role; the pool of individuals range in their proficiency level for the job from 46% to 68%. This suggests that the strongest candidate from that group has a proficiency level of 68%. If an organisation’s recruitment criterion requires a candidate to have a proficiency level of at least 65%, then there would be a very small number of individuals left over to be considered for the role. However, these potential individuals may not meet other requirements of the employment, such as eligibility for work in the country, and thus the vacancy is very unlikely to be filled.
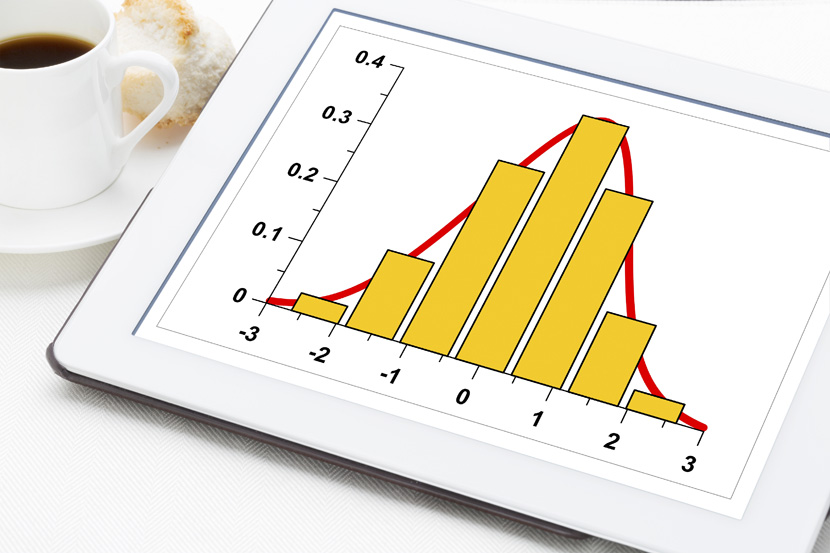
Normal Distribution
Norms are developed through extensive research and administration of a particular psychometric tool to a large (at least 200) group of similar individuals (e.g. graduates), following which the distribution of these scores are considered. Often these scores will fall in a ‘normal distribution’ (see chapter ), a statistical requirement for the norms to be used in this manner. Using the example of an ability test, this type of distribution suggests that “most” individuals will get a score around the average on the test, with a very small number getting either a very poor (low) score or a very high score.
As such, for any group of individuals there is a range of scores; here is an example:
In an ability test with 20 questions, the possible score range could be 0 to 20, however after administering the test to a group of individuals, we may find that no one got a score of less than 2, nor did any candidate achieve a score greater than 18. Thus the range of scores for this group would be 2 to 18. Using a life example, the heights of adults in the UK would also produce a normal distribution, with most people in the middle (average height of around 5’6”) and very few adults with heights of 7’8” (extreme right of curve) and also very few adults with heights of 3’2” (extreme left of curve).
Assuming the above norm group is that of graduates, then a graduate who applies for a job role may be compared against a representative group (norm) of graduates who have completed the test previously; this would help provide meaningfulness to their score. According to the above norm group, a candidate who obtains a score of 18 or more would have done better than 99% of the comparison (norm) group. In a similar light a candidate who gets a score of 11 will have done better than at least 50% of similar graduates.
Percentiles and Standard Deviation
Each distribution curve covers 100 % of the individuals who took the test. If the curve was split in half, we would find that 50% of the individuals did worse than average (the middle point of the curve) and 50% did better than average. Once we begin to rank individuals on their performance, we can start talking about percentiles – how many individuals did the candidate do better than.
The graph depicts a normal distribution that has been sliced in to 6 pieces (see image at top of screen). The values in the graph tell you the percentage of people that sit in that section. The values of -3 to +3 are simply a scale that tells us about how the scores are spread, also known as the standard deviation (SD). An individual who gets a score of +1 SD will have done better than 84% of the individuals in the comparison group. This scale simply helps us to begin identifying where individuals sit on the curve and what that means in terms of their performance. This is the basis behind norming.
Norming therefore allows an organisation to select the best of what is available as individual performances on a particular test are benchmarked against a larger representative group which provides an indication of their potential in comparison to others. This way an organisation may choose to consider the top 50% of candidates by sending them through to the next stages of a recruitment process; this methodology satisfies an organisation’s recruitment needs, but keeps the best talent of what is available.








